Shortest and simplest guide to perform feature selection with Lasso Regression in Python.
Lasso Regression to perform feature selection?
While trying to minimize the cost function, Lasso regression will automatically select those features that are useful, discarding the useless or redundant features. In Lasso regression, discarding a feature will make its coefficient equal to 0. Also, Lasso Regression makes the model more generalizable to unseen samples.
How to Perform it in Scikit-Learn?
Logistic Regression in sklearn performs Ridge Regression ( L2 regularization) by default which manages overfitting very well but will not make coefficient equal to zero and it will not help us in removing redundant features and this is a Key difference between Ridge and Lasso regression. To call For Lasso Regression( L1 Regularization) we need to specify penalty= ‘ l1 ’ while calling Logistic Regression.
We will choose the best C value i.e. Inverse of regularization strength by finetuning it, Typically we explore values between 0 and 1 although values greater than 1 are also acceptable.
We will store the number of non-zero coefficients and metrics such as Accuracy, Precision, Recall, and F1_score which will give a broader idea of how many features are Non-Zero (Selected) and what was the corresponding metrics for the model.
Considering that we have already performed our train test split, we will directly jump to our main goal.
#Listing all values we want to try as C value
C=[1,0.75,0.50, 0.25, 0.1,0.05, 0.025, 0.01, 0.005, 0.0025]
#Intiate Metric of zeros with 6 columns and and rows equal to len(C)
l1_metrics=np.zeros((len(C),6))
#Adding first column as value C
l1_metrics[:,0]=C
# Run a for loop over the range of C list length
for index in range(0, len(C)):
# Initialize and fit Logistic Regression with the C candidate
logreg = LogisticRegression(penalty='l1', C=C[index], solver='liblinear')
logreg.fit(X_train, y_train)
# Predict on the testing data
y_pred = logreg.predict(X_test)
# Create non-zero count and all metrics columns
l1_metrics[index,1] = np.count_nonzero(logreg.coef_)
l1_metrics[index,2] = accuracy_score(y_test, y_pred)
l1_metrics[index,3] = precision_score(y_test, y_pred)
l1_metrics[index,4] = recall_score(y_test, y_pred)
l1_metrics[index,5] = f1_score(y_test, y_pred)Let’s print the output
# Name the columns and print the array as pandas DataFrame
col_names = ['C','Non-Zero Coeffs','Accuracy','Precision','Recall','F1_score']
print(pd.DataFrame(l1_metrics, columns=col_names))
How to Choose the best value for C?
We can see lowest C value shrinks the number of non-zero coefficients while also impacting the performance of metrics. The decision on which C value to choose depends on the cost of declining Precision and/ or Recall.
Typically we would like to choose a model with reduced complexity that still maintains similar performance metrics.
In our case, the C value of 0.1 meets this criterion it reduces the number of features to 17 while maintaining similar performance to the one with non- regularized models.
Other models with lower C start experiencing a decline in Accuracy and all other metrics
How to get all selected features and their importance?
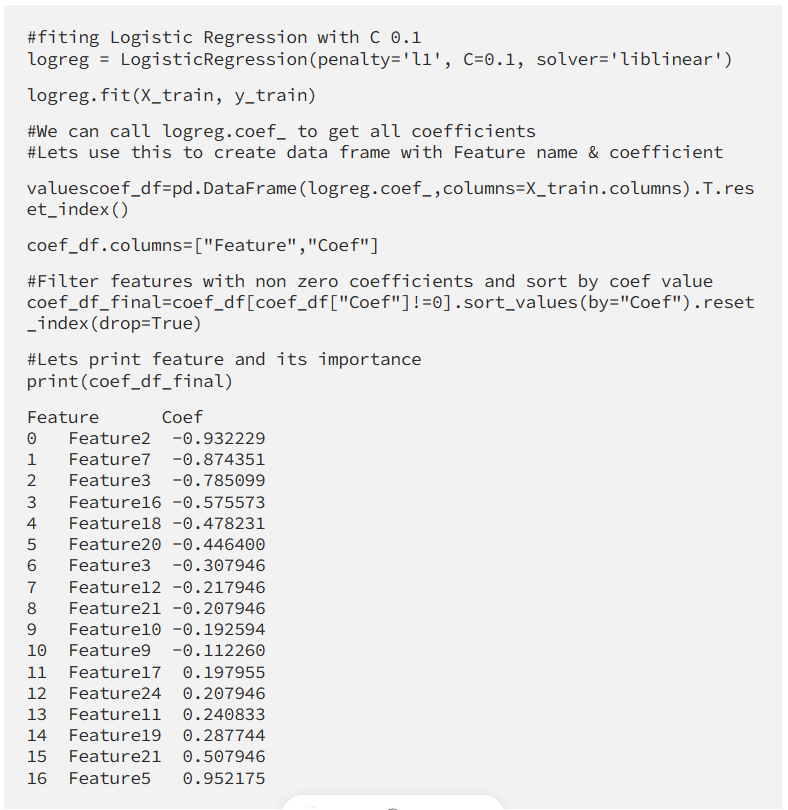
Conclusion
Congratulations!
We have selected the most important feature from our data set. As we see Lasso Regression is one of the simplest and most robust methods of selecting important features while maintaining similar performance to the one with non- regularized models this is also a great way to show your non-technical stockholders which factors are most important.
Hope this article help fellow Data Scientist and aspirants
Thanks for reading this article! Don’t forget to leave a comment 💬!


Great Article, thank you for sharing 🙂